One Of The Best Info About How To Detect Multicollinearity

As a rule of thumb, a condition number between 10 and 30 indicates the. Now we run a multiple regression analysis using spss. This video explains the concept of multicollinearity in a multiple regression model.the video explains how to detect multicollinearity in e views and how to.

how to lose inches off your hips fast how to learn drum tabs how to recover deleted files on a hard drive how to improve hdl how to keep a diary online how to increase amps how to sell my small business how to repair water damage floor

Multicollinearity - Explained Simply (part 1) Youtube

Multicollinearity Detection - Youtube

Multicollinearity In Regression Analysis: Problems, Detection, And Solutions - Statistics By Jim

Multicollinearity - Youtube

Multicollinearity - Definition, Types, Regression, Examples

Multicollinearity - Cfa, Frm, And Actuarial Exams Study Notes

The most common way to detect multicollinearity is by using the variance inflation factor (vif), which measures the correlation and strength of.

How to detect multicollinearity. We obtain the following results: For a given predictor (p), multicollinearity can assessed by computing a score called the variance inflation factor (or vif ), which measures how much the variance of a. A simple method to detect multicollinearity in a model is by using something called the variance inflation factor or the vif for each predicting variable.

If it’s above.8 (or.7 or.9 or some other high number), the rule of thumb says you have multicollinearity. How to detect multicollinearity easily. At first sight it looks like a.

Next we will examine multicollinearity through the varianceinflation factor and tolerance. Review scatterplot and correlation matrices. This can be done by specifying the “vif”, “tol”, and “collin” options after the.

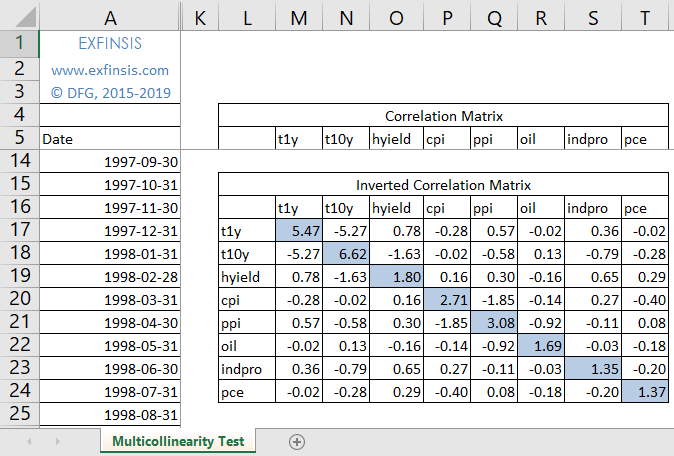
The best way to identify the multicollinearity is to calculate the variance inflation factor (vif) corresponding to every independent variable in the dataset. The best way to detect collinearity in the linear regression model is the multicollinearity variance inflation factor (vif), calculated to figure out the standard of tolerance and assess the degree. To detect multicollinearity, we use the condition number (i.e., the largest condition index).

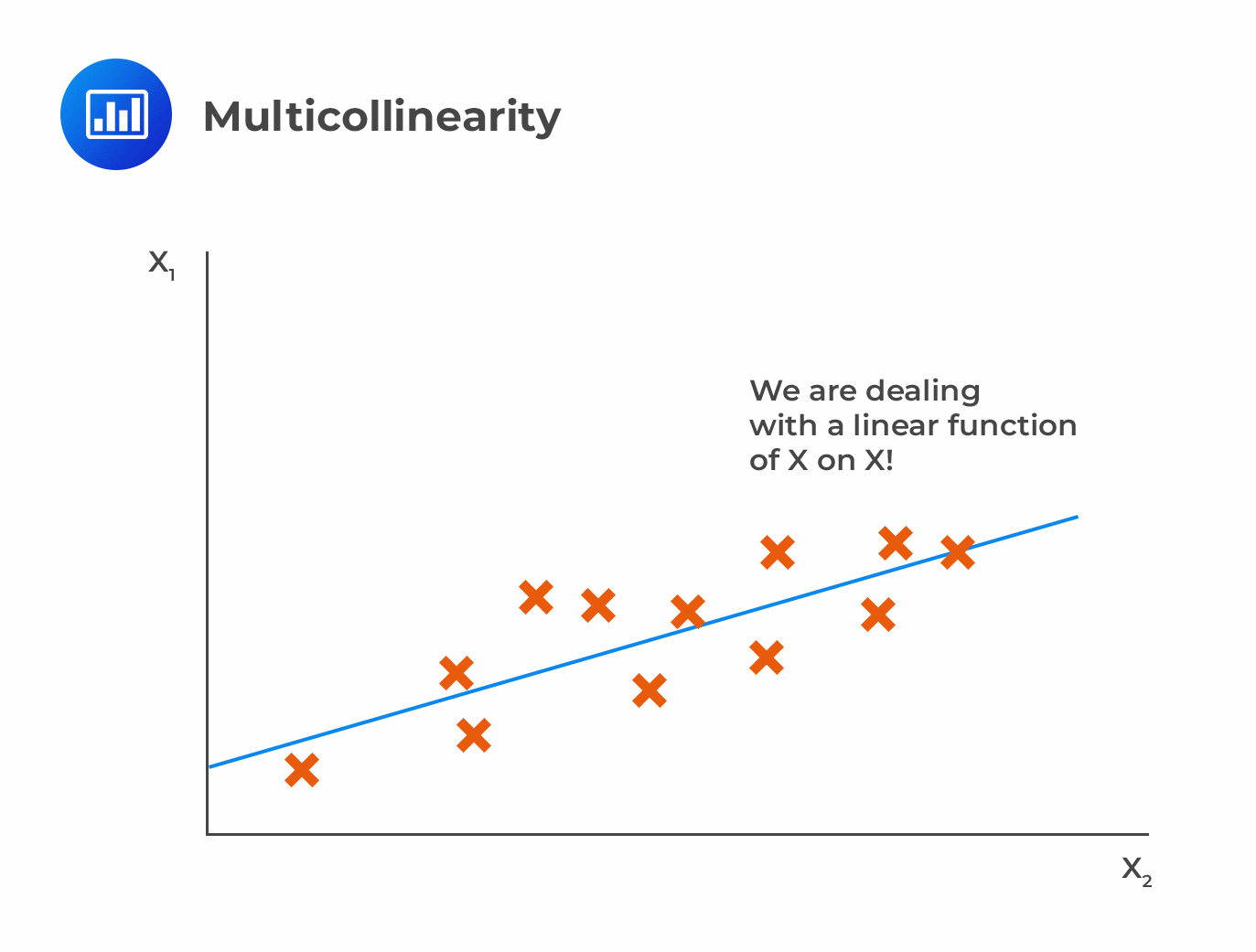
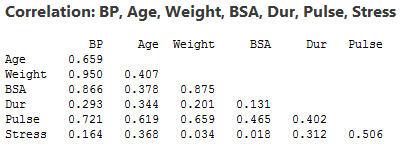
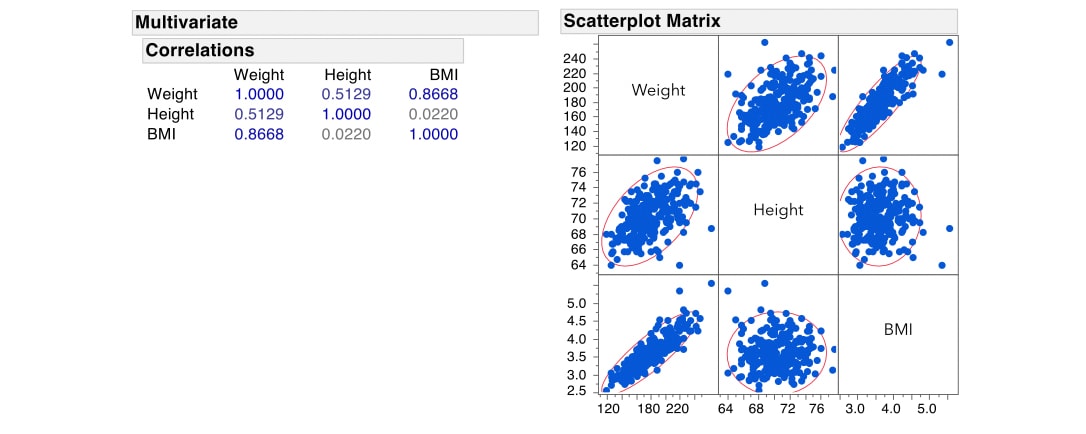
Printing and observing bivariate correlations of predictors is not good enough when evaluating the existence of multicollinearity because of. In the last blog, i mentioned that a scatterplot matrix can show. One way to detect multicollinearity is by using a metric known as the variance inflation factor (vif), which measures the correlation and strength of correlation between the.

The analysis exhibits the signs of multicollinearity. Some of the common methods used for detecting multicollinearity include: Variance inflating factor (vif) is used to test the presence of multicollinearity in a regression model.